Memahami grafik trigonometri merupakan salah satu aspek penting dalam mempelajari materi trigonometri. Grafik ini membantu visualisasi fungsi trigonometri, sehingga memudahkan dalam menganalisis perilaku dan karakteristiknya.
Dengan mempelajari grafik trigonometri, siswa dapat memahami bagaimana fungsi trigonometri bekerja dan bagaimana mereka dapat diterapkan dalam berbagai bidang, seperti fisika, teknik, dan lain-lain.
Pemahaman yang baik tentang grafik trigonometri juga membantu dalam mengembangkan kemampuan analitis dan pemecahan masalah.
Intisari
- Memahami konsep dasar grafik trigonometri
- Menganalisis perilaku fungsi trigonometri
- Mengaplikasikan grafik trigonometri dalam berbagai bidang
- Mengembangkan kemampuan analitis dan pemecahan masalah
- Meningkatkan pemahaman tentang materi trigonometri
Pendahuluan Grafik Trigonometri
Grafik trigonometri merupakan alat visual yang powerful dalam memahami hubungan antara sudut dan nilai trigonometri. Dengan menggunakan grafik, kita dapat lebih mudah menganalisis dan memahami berbagai konsep trigonometri.
Apa itu Grafik Trigonometri?
Grafik trigonometri adalah representasi visual dari fungsi trigonometri, seperti sinus, kosinus, dan tangen. Grafik ini membantu dalam memahami bagaimana nilai trigonometri berubah terhadap sudut.
Pentingnya Grafik dalam Trigonometri
Grafik trigonometri penting karena memvisualisasikan hubungan antara sudut dan nilai trigonometri, sehingga memudahkan analisis dan penerapan konsep trigonometri. Dengan grafik, kita dapat memahami beberapa aspek penting, seperti:
- Memahami periode dan amplitudo fungsi trigonometri.
- Menganalisis perubahan nilai trigonometri terhadap sudut.
- Mengaplikasikan konsep trigonometri dalam berbagai bidang, seperti fisika dan teknik.
Dengan demikian, grafik trigonometri menjadi alat yang sangat berharga dalam mempelajari dan menerapkan trigonometri.
Fungsi Trigonometri Dasar
Grafik trigonometri tidak dapat dipisahkan dari fungsi trigonometri dasar yang meliputi sinus, kosinus, dan tangen. Memahami ketiga fungsi ini adalah kunci untuk menganalisis dan menginterpretasikan grafik trigonometri dengan benar.
Sinus
Fungsi sinus adalah salah satu fungsi trigonometri dasar yang paling penting. Sinus dari suatu sudut dalam segitiga siku-siku didefinisikan sebagai perbandingan antara panjang sisi yang berlawanan dengan sudut tersebut dan panjang hipotenusa.
Kosinus
Fungsi kosinus juga merupakan fungsi trigonometri dasar yang sangat penting. Kosinus dari suatu sudut didefinisikan sebagai perbandingan antara panjang sisi yang berdekatan dengan sudut tersebut dan panjang hipotenusa.
Tangen
Fungsi tangen adalah fungsi trigonometri yang didefinisikan sebagai perbandingan antara sinus dan kosinus dari suatu sudut. Tangen sangat berguna dalam berbagai aplikasi trigonometri.
Berikut adalah tabel perbandingan antara fungsi sinus, kosinus, dan tangen:
| Fungsi | Definisi | Aplikasi |
|---|---|---|
| Sinus | Perbandingan sisi lawan dan hipotenusa | Analisis gelombang, getaran |
| Kosinus | Perbandingan sisi dekat dan hipotenusa | Analisis gelombang, proyeksi vektor |
| Tangen | Perbandingan sinus dan kosinus | Pengukuran kemiringan, analisis trigonometri |
Dengan memahami fungsi-fungsi trigonometri dasar ini, kita dapat lebih mudah memahami grafik trigonometri dan berbagai aplikasinya dalam matematika dan sains.
Karakteristik Grafik Fungsi Trigonometri
Grafik fungsi trigonometri memiliki beberapa karakteristik penting yang perlu dipahami. Karakteristik ini membantu dalam menganalisis dan menginterpretasikan grafik dengan lebih baik.
Periode
Periode adalah jarak antara dua titik yang berurutan pada grafik yang memiliki fase yang sama. Fungsi trigonometri seperti sinus dan kosinus memiliki periode $2\pi$. Mengerti periode membantu dalam memahami siklus trigonometri dan bagaimana grafik berulang.
Amplitudo
Amplitudo adalah ukuran seberapa tinggi atau rendah grafik fungsi trigonometri dari garis tengahnya. Amplitudo didefinisikan sebagai setengah dari jarak antara nilai maksimum dan minimum fungsi.
- Amplitudo mempengaruhi seberapa “tinggi” atau “rendah” grafik.
- Nilai amplitudo yang lebih besar berarti grafik lebih “terentang” secara vertikal.
Asimptot
Asimptot adalah garis yang didekati oleh grafik fungsi tanpa pernah menyentuhnya. Fungsi tangen memiliki asimptot vertikal pada titik-titik tertentu.
Grafik Fungsi Sinus
Fungsi sinus merupakan salah satu konsep dasar dalam trigonometri yang memiliki aplikasi luas dalam berbagai bidang.
Dalam mempelajari grafik fungsi sinus, kita akan membahas definisi dan penerapan fungsi ini dalam berbagai konteks.
Definisi dan Penerapan
Fungsi sinus didefinisikan sebagai rasio antara panjang sisi lawan sudut terhadap panjang sisi miring dalam sebuah segitiga siku-siku.
Fungsi sinus memiliki sifat periodik dengan periode 360 derajat atau 2π radian, membuatnya sangat berguna dalam memodelkan fenomena alam yang berulang.
Dalam fisika, fungsi sinus digunakan untuk menggambarkan gelombang suara, gelombang cahaya, dan berbagai jenis osilasi lainnya.
Contoh Grafik Sinus
Berikut adalah contoh grafik sinus yang menggambarkan fungsi sinus dalam satu periode.
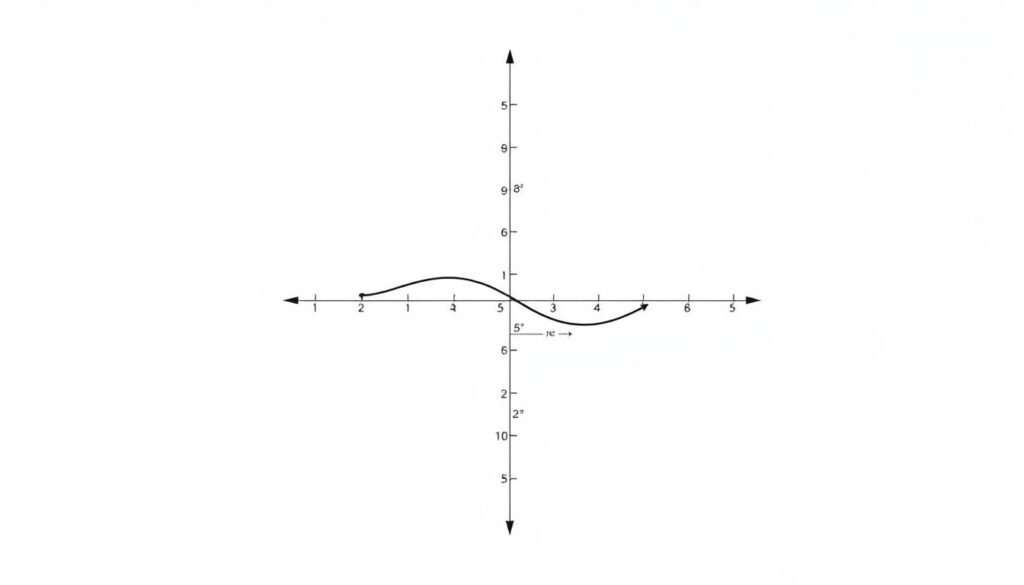
Grafik di atas menunjukkan bagaimana nilai fungsi sinus berubah terhadap sudut dalam satu periode penuh.
| Sudut (derajat) | Nilai Sinus |
|---|---|
| 0 | 0 |
| 90 | 1 |
| 180 | 0 |
| 270 | -1 |
| 360 | 0 |
Dari tabel di atas, kita dapat melihat bagaimana nilai fungsi sinus berubah pada sudut-sudut tertentu.
Dengan memahami grafik fungsi sinus, kita dapat lebih mudah menganalisis berbagai fenomena yang melibatkan perubahan periodik.
Grafik Fungsi Kosinus
Grafik fungsi kosinus digunakan untuk menganalisis berbagai fenomena periodik dalam ilmu pengetahuan. Fungsi kosinus memiliki karakteristik unik yang membedakannya dari fungsi trigonometri lainnya.
Definisi dan Penerapan
Fungsi kosinus didefinisikan sebagai rasio antara sisi yang berdekatan dengan sudut dan hipotenusa dalam sebuah segitiga siku-siku. Grafik kosinus digunakan dalam berbagai bidang seperti fisika, teknik, dan pengolahan data untuk menganalisis perubahan periodik.
Penerapan fungsi kosinus meliputi analisis gelombang suara, pemrosesan sinyal, dan pemodelan fenomena alam yang berulang.
Contoh Grafik Kosinus
Grafik kosinus memiliki bentuk gelombang yang khas, dengan nilai maksimum dan minimum yang berulang pada interval tertentu. Contoh grafik kosinus dapat dilihat pada analisis gelombang sinusoidal dalam fisika.
- Grafik kosinus digunakan untuk memodelkan perubahan periodik.
- Fungsi kosinus membantu dalam menganalisis data yang berulang.
Grafik Fungsi Tangen
Grafik fungsi tangen adalah salah satu konsep penting dalam trigonometri yang memiliki karakteristik unik. Fungsi tangen, yang didefinisikan sebagai perbandingan antara sinus dan kosinus, memiliki peran penting dalam berbagai aplikasi matematika dan ilmu pengetahuan.
Definisi dan Penerapan
Fungsi tangen didefinisikan sebagai tan(x) = sin(x) / cos(x). Fungsi ini memiliki penerapan luas dalam berbagai bidang, termasuk navigasi, fisika, dan teknik. Grafik tangen membantu dalam memahami bagaimana nilai tangen berubah terhadap sudut.
Contoh Grafik Tangen
Grafik fungsi tangen memiliki bentuk yang khas dengan asimptot vertikal pada titik-titik tertentu. Berikut adalah contoh sederhana grafik tangen:
Perhatikan bagaimana grafik tangen mendekati tak terhingga saat mendekati asimptot.
X dan Y Asymptote
Asimptot pada grafik tangen terjadi pada nilai x yang membuat cos(x) = 0, yaitu pada x = π/2 + kπ, dengan k sebagai bilangan bulat. Asimptot ini membagi grafik menjadi beberapa bagian yang berulang.
| Nilai x | Nilai tan(x) | Keterangan |
|---|---|---|
| π/4 | 1 | Tangen positif |
| π/2 | Tak Terdefinisi | Asimptot Vertikal |
| 3π/4 | -1 | Tangen negatif |
Dengan memahami asimptot dan perilaku grafik tangen, kita dapat lebih baik menganalisis fungsi trigonometri dalam berbagai konteks.
Transformasi Grafik Trigonometri
Transformasi grafik trigonometri memungkinkan penyesuaian grafik untuk berbagai keperluan analisis dengan cara memodifikasi bentuk dan posisi grafik. Dengan memahami cara melakukan transformasi ini, kita dapat lebih fleksibel dalam menganalisis dan menerapkan fungsi trigonometri.
Pergeseran Vertikal dan Horizontal
Pergeseran grafik trigonometri dapat dilakukan secara vertikal dan horizontal. Pergeseran vertikal terjadi ketika grafik digeser ke atas atau ke bawah, sedangkan pergeseran horizontal terjadi ketika grafik digeser ke kiri atau ke kanan.
Contoh pergeseran vertikal dapat dilihat pada fungsi y = sin(x) + c, di mana c adalah konstanta yang menentukan besar pergeseran. Jika c positif, grafik bergeser ke atas; jika c negatif, grafik bergeser ke bawah.
| Fungsi | Pergeseran |
|---|---|
| y = sin(x) + 2 | Pergeseran 2 satuan ke atas |
| y = sin(x) – 1 | Pergeseran 1 satuan ke bawah |
| y = sin(x + π/2) | Pergeseran π/2 satuan ke kiri |
| y = sin(x – π/2) | Pergeseran π/2 satuan ke kanan |
Perubahan Amplitudo dan Periode
Selain pergeseran, transformasi grafik trigonometri juga dapat dilakukan dengan mengubah amplitudo dan periode. Amplitudo adalah ukuran seberapa tinggi dan rendah grafik berosilasi, sedangkan periode adalah jarak antara dua puncak atau lembah yang berurutan.
Perubahan amplitudo dapat dilakukan dengan mengalikan fungsi trigonometri dengan suatu konstanta, misalnya y = a*sin(x), di mana a adalah amplitudo baru. Periode dapat diubah dengan mengalikan argumen fungsi trigonometri, seperti y = sin(b*x), di mana periode baru adalah 2π/b.
Dengan memahami transformasi grafik trigonometri, kita dapat menganalisis berbagai fenomena yang melibatkan fungsi trigonometri dengan lebih baik. Transformasi ini memungkinkan penyesuaian model matematika untuk berbagai aplikasi nyata.
Aplikasi Grafik Trigonometri dalam Kehidupan Nyata
Grafik trigonometri memainkan peran kunci dalam memahami dan menganalisis berbagai fenomena alam dan proses teknis. Dengan kemampuan untuk memodelkan osilasi dan gelombang, grafik trigonometri digunakan dalam berbagai bidang.
Dalam Ilmu Fisika
Dalam ilmu fisika, grafik trigonometri digunakan untuk menggambarkan gerakan harmonik sederhana, seperti pendulum dan pegas. Fungsi sinus dan kosinus digunakan untuk memodelkan osilasi ini.
Contoh lainnya adalah dalam analisis gelombang suara dan cahaya, di mana fungsi trigonometri membantu dalam memahami sifat-sifat gelombang tersebut.
| Konsep Fisika | Aplikasi Trigonometri |
|---|---|
| Gerakan Harmonik Sederhana | Fungsi Sinus dan Kosinus |
| Gelombang Suara dan Cahaya | Analisis Frekuensi dan Amplitudo |
Dalam Teknik dan Rekayasa
Dalam teknik dan rekayasa, grafik trigonometri digunakan dalam analisis struktur, seperti jembatan dan bangunan, untuk memahami distribusi gaya dan tekanan.
Selain itu, dalam teknik elektro, trigonometri digunakan dalam analisis sinyal dan sistem komunikasi.

Dalam Pengolahan Data
Dalam pengolahan data, grafik trigonometri digunakan dalam analisis deret waktu dan pengolahan sinyal. Teknik seperti transformasi Fourier menggunakan fungsi trigonometri untuk menganalisis frekuensi dalam data.
Dengan demikian, grafik trigonometri membantu dalam mengidentifikasi pola dan tren dalam data yang kompleks.
Kesimpulan
Memahami grafik trigonometri membuka peluang untuk eksplorasi lebih lanjut dalam matematika dan bidang terkait. Dengan mempelajari materi trigonometri, kita dapat menganalisis berbagai fenomena alam dan menerapkan konsep-konsep matematika dalam berbagai disiplin ilmu.
Konsep Utama
Grafik trigonometri merupakan representasi visual dari fungsi trigonometri yang meliputi sinus, kosinus, dan tangen. Karakteristik grafik ini mencakup periode, amplitudo, dan asimptot. Dengan memahami konsep-konsep ini, kita dapat menerapkan grafik trigonometri dalam berbagai aplikasi, seperti dalam ilmu fisika, teknik, dan rekayasa.
Pembelajaran Selanjutnya
Untuk memperdalam pemahaman tentang grafik trigonometri, disarankan untuk mempelajari transformasi grafik trigonometri dan menerapkan konsep-konsep ini dalam berbagai masalah matematika dan bidang terkait. Dengan demikian, kita dapat meningkatkan kemampuan analisis dan penerapan konsep matematika dalam berbagai situasi.
FAQ
Apa itu grafik trigonometri?
Grafik trigonometri adalah representasi visual dari fungsi trigonometri yang membantu memahami perilaku dan karakteristik fungsi-fungsi tersebut.
Mengapa grafik trigonometri penting dalam mempelajari trigonometri?
Grafik trigonometri membantu memvisualisasikan hubungan antara sudut dan nilai trigonometri, sehingga memudahkan analisis dan penerapan konsep trigonometri.
Apa saja fungsi trigonometri dasar yang dibahas dalam grafik trigonometri?
Fungsi trigonometri dasar yang dibahas dalam grafik trigonometri adalah sinus, kosinus, dan tangen.
Bagaimana cara menganalisis grafik fungsi sinus?
Grafik fungsi sinus dapat dianalisis dengan memahami definisi, penerapan, dan karakteristik seperti amplitudo dan periode.
Apa itu titik stasioner dalam grafik trigonometri?
Titik stasioner dalam grafik trigonometri adalah titik di mana fungsi trigonometri memiliki nilai maksimum atau minimum.
Bagaimana transformasi grafik trigonometri dilakukan?
Transformasi grafik trigonometri dapat dilakukan melalui pergeseran vertikal dan horizontal, serta perubahan amplitudo dan periode.
Apa saja aplikasi grafik trigonometri dalam kehidupan nyata?
Grafik trigonometri digunakan dalam berbagai bidang seperti ilmu fisika, teknik, rekayasa, dan pengolahan data untuk memodelkan fenomena alam dan proses teknis.
Bagaimana cara menghitung turunan fungsi trigonometri?
Turunan fungsi trigonometri dapat dihitung menggunakan aturan turunan yang sesuai untuk setiap fungsi trigonometri.
Apa itu siklus trigonometri?
Siklus trigonometri merujuk pada periode atau pengulangan nilai-nilai trigonometri dalam suatu interval tertentu.
